Solución del Examen de Admisión Universidad del Cauca 2013-2

 

Examen de Admisión Universidad del Cauca 2013-2
SOLUCIÓN DE LAS PREGUNTAS DE RAZONAMIENTO LOGICO
41. De un grupo de estudiantes bachilleres que piensan presentar el examen de admisión a una universidad se sabe que 1/3 se presentará a medicina, 7/12 se presentará a psicología y 1/8 se  presentará a ambas carreras. Si el resto, que son 15 estudiantes, aun no deciden a qué carrera presentarse, el número total de estudiantes es:
A) 84     B) 72     C) 63      D) 90



42. De un grupo de 4 personas que van a comer a un restaurante se sabe que tres personas piden sopa, tres piden carne, tres piden jugo, y solo una persona pide sopa, carne y jugo. El número de personas que pidieron sopa y carne, y no pidieron jugo es:
A) 0     B) 1     C) 2    D) 3



43. De 76 estudiantes que pueden matricularse en los cursos de álgebra, geometría y cálculo. Se sabe que 42 se matricularon en álgebra, 30 en geometría y 28 en cálculo. Uno se matriculó en los tres cursos. Si todos tomaron al menos un curso, el número de estudiantes que se matriculó solo en 2 de los cursos fue:
A) 22      B) 18      C) 20     D) 24

44. Ana debe comprar frutas para llevar a su casa. Se sabe que si compra peras o manzanas entonces también debe comprar ciruelas o guayabas. Pero si no consigue manzanas, entonces compra ciruelas. Sin embargo, decide no llevar ciruelas. Las frutas que necesariamente compra Ana son:
A) Peras
B) Manzanas y guayabas
C) Peras y guayabas
D) Peras y manzanas

45. Se debe determinar el mayor de tres números pares consecutivos y se tienen las siguientes informaciones:
I. El promedio de dos de ellos es igual al tercero
II. El menor de ellos es un número primo
Para resolver el problema:
A) La información I es suficiente y la II no lo es
B) La información II es suficiente y la I no lo es
C) Es necesario utilizar I y II conjuntamente
D) Cada uno de los datos, por separado, es suficiente

46. En una caja hay 30 objetos entre pelotas, cubos y trompos. Cada objeto es de un solo color, que puede ser: verde, amarillo o azul. Hay igual cantidad de objetos de cada color. Se sabe que :
• Hay 8 cubos y 7 trompos
• Hay igual cantidad de pelotas de cada color
• No hay cubos verdes
• No hay trompos amarillos
Entonces se cumple que hay:
A) 3 cubos azules                B) 5 trompos azules
C) 3 cubos amarillos           D) 2 trompos verdes

47. La siguiente tabla muestra algunos resultados de un triangular de futbol jugado en una sola vuelta:
Equipos  GF     GC   Puntos
Tigres      1          0       4
Ases        1         1        2
Águilas    1         2       1   
GF: Goles a favor / GC: Goles en contra
El puntaje se asigna así: Un partido ganado da 3 puntos, un partido empatado 1 punto y un partido perdido O puntos.
El resultado del partido Ases y Águilas fue:
A) 1-0        B) 1-1       C) 0-0       D) 2-1

Preguntas 48 a 50
Tres amigas Alejandra, Isabela y Camila juegan a las estatuas, este juego consiste en quedarse quieto en una posición e ir eliminando a los jugadores que realicen algún movimiento, el orden de eliminación determina el orden para la asignación de puntos. En cada ronda la ganadora obtiene tres puntos, la que queda en segundo lugar obtiene un punto y la que queda en último lugar no obtiene ninguno (nunca hay empate)
48. Si se juegan cuatro rondas y se sabe que todas ellas ganaron al menos una, entonces de las siguientes afirmaciones la única que NO es posible es:
A) La que más rondas ganó obtuvo el doble de puntos que otra de ellas
B) Una de ellas obtuvo 6 puntos y otra obtuvo 7 puntos
C) La que más rondas ganó obtuvo el mismo puntaje que otra de ellas
D) Las tres obtuvieron el mismo puntaje

49. Si se juegan 4 rondas y se sabe que Isabela ganó tres de ellas, entonces de las siguientes afirmaciones la única que NO es posible es:
A) Alejandra obtuvo tres puntos
B) Camila obtuvo un punto
C) Camila no ganó ninguna ronda pero obtuvo más puntos que Alejandra
D) Los puntos obtenidos por Camila y Alejandra superan los obtenidos por Isabela

50.  Si después de 4 rondas Alejandra tiene 5 puntos y Camila tiene 4 puntos, entonces el número de rondas que ganó Isabela fue:
A) 0       B) 1       C) 2       D) 3

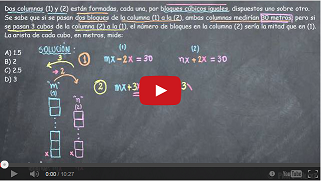
51. Dos columnas (1) y (2) están formadas, cada una, por bloques cúbicos iguales, dispuestos uno sobre otro. Se sabe que si se pasan dos bloques de la columna (1) a la (2), ambas columnas medirían 30 metros, pero si se pasan 3 cubos de la columna (2) a la (1), el número de bloques en la columna (2) sería la mitad que en (1). La arista de cada cubo, en metros, mide:
A) 1.5       B) 2        C) 2.5         D) 3

52.  Al finalizar un torneo de fútbol fueron premiados los jugadores que hicieron 13, 14 y 15 goles. El número total de goles realizados por los premiados fue 125 y entre estos jugadores solamente 5 hicieron más de 13 goles. El número de jugadores que hicieron 15 goles fue:
A) 1      B) 2     C) 3     D) 4

53. En la gráfica se ilustran los porcentajes de aprobación a las políticas de gobierno de los últimos cinco alcaldes A, B, C, D y E de una ciudad, por parte de un grupo de ciudadanos encuestados, donde las opciones de respuesta únicamente son "aprueba" o "desaprueba".
 De las siguientes afirmaciones:
I. El porcentaje promedio de encuestados que desaprueban las políticas de gobierno por alcalde es 40%.
II. El 75% de los encuestados que aprueban las políticas del alcalde A es igual al porcentaje de los que aprueban a B.
III. El porcentaje de encuestados que desaprueban las políticas del alcalde D es igual a 60% del porcentaje de encuestados que aprueban las del alcalde C.
Es verdadera:
A) Solo I         B) Solo II        C) Solo III        D) Solo II y III



Un comerciante vendió parte de la mercancía que llevaba en tres lugares distintos. Cada unidad de su mercancía la vendió a $900. En el primer lugar vendió el 10% de la cantidad inicial que llevaba. En el segundo lugar vendió el 20% de la mercancía restante, y en el tercer lugar vendió el 50% de lo que le quedaba.
54. El porcentaje de la cantidad inicial que corresponde al total vendido por el comerciante es:
A) 80%       B) 60%        C) 64%       D) 72%

56.  En un grupo de 20 estudiantes se hizo un estudio sobre el tiempo que usan computador en distintas actividades. El promedio obtenido fue de 40 horas por semana. Si no se hubiera tenido en cuenta el dato de 2 estudiantes en particular, el promedio habría disminuido en un 5%. El promedio de tiempo usado por estos dos estudiantes, en horas por semana, es:
A) 58      B) 45      C) 50.5      D) 52

57.  En un pueblo las placas de los automóviles constan de dos letras y dos dígitos. Las letras de cada placa deben ser distintas y se escogen entre 5 posibles y los dos dígitos deben ser diferentes. El número total de placas que pueden fabricarse es:
A) 850      B) 1000      C) 1250      D) 1800

58. Una bolsa completamente oscura contiene 20 bolas numeradas del 1 al 20. El número mínimo de bolas que se deben extraer al azar para tener la certeza de que entre las bolas extraídas se encuentre una numerada con un número impar menor que 9 es:
A) 15      B) 16      C) 17       D) 18

Preguntas 59 a 60
A una fiesta asisten 11 personas, 5 de las cuales NO bailan.
59. El número total de maneras en las que es posible seleccionar dos personas que no bailen es:
A) 5      B) 10        C) 15       D) 20

60.  Se seleccionan al azar a dos personas de la fiesta. La probabilidad de que las personas seleccionadas no bailen es:
A) 1/11        B) 2/11         C) 4/11        D) 5/11

61.  Un profesor de matemáticas quiere garantizar que en su clase haya al menos 20 niños o 20 niñas. El número mínimo de alumnos que debe tener este profesor para garantizarlo es:
A) 21      B) 39      C) 40      D) 41



62.  Julián tiene en la semana dos clases de natación, una clase de dibujo y una clase de inglés. Si Julián quiere tomar estas clases de lunes a jueves, tomar sólo una clase por día y no tener las clases de natación dos días seguidos, entonces el número de formas en que puede organizar sus clases, es:
A) 3        B) 4        C) 6        D) 8

63.  Se escriben todos los números impares entre 1 y 99 (incluyéndolos) y se hace el producto de todos ellos. El dígito de las unidades del resultado de este producto es:
A) 3       B) 5        C) 7      D) 9



64. Laura tiene un perrito cuya edad en meses es la mitad de la edad de Laura en años. Dentro de cinco años la edad del perrito en meses será cinco más que el doble de la edad de Laura en años. Entonces, la edad actual del perrito de Laura, en meses, es:
A) 18        B) 15       C) 13      D) 11

65. Lina sale de su casa con dos cantidades de dinero así: una suma para sus gastos propios y $ 15.000 para prestarlos a su amiga Diana. Inicialmente gasta el 50% de la suma de gastos propios en materiales de trabajo. Posteriormente invitó a una amiga a almorzar y al solicitar la cuenta, ésta costaba el 50% del total de la suma del dinero que le quedaba para sus gastos propios más lo que iba a prestarle a Diana. Si después de pagar la cuenta solo le quedan $ 12.000 de lo que debía prestarle a Diana, entonces, la suma inicial para sus gastos propios en pesos, es:

A) 25.000         B) 22.000          C) 18.000          D) 15.000

66. Se define la expresión S(a) = a + (a+1)/(a+2)+(a+2)/(a+3) para todo a entero y a ≥ 1. De las afirmaciones siguientes, la única verdadera para todo valor de a, es
A) a+0.5 < S(a) < a+1.5
B) a < S(a) < a+1
C) a < S(a) < a+2
D) a+2 < S(a) < a+3

Preguntas 67 a 68
Un teatro tiene un total de 30 filas. La primera fila tiene 14 sillas y cada una de las filas siguientes tiene dos sillas más que la anterior.
67.  El número de sillas de más que la fila número 30, tiene con respecto a la primera fila, es:
A) 72      B) 64      C) 58      D) 46

68. Si las sillas están numeradas en orden creciente empezando por la primera fila de izquierda a derecha, iniciando en el número 1 y siguiendo la secuencia de los números naturales y continuando con la segunda fila, siempre de izquierda a derecha, entonces, la fila donde está ubicada la silla correspondiente al número 100 es:

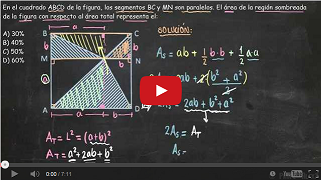
A) La 4       B) La 6       C) La 8       D) La 9

69. En el cuadrado ABCD de la figura, los segmentos BC y MN son paralelos. El área de la región sombreada de la figura con respecto al área total representa el:
A) 30%      B) 40%        C) 50%       D) 60%

70. Sobre cada cara de un cubo se pintan 10 puntos, de manera tal que sobre cada arista quedan dos puntos pintados. El número total de puntos pintados es:
A) 26       B) 28       C) 36      D) 60

71. En la figura se ilustran dos circunferencias con centro P y Q y radio 1 cm cada una. El área, en cm2, de la región sombreada es:
A) √3/2       B) √2       C) 2√3      D) √3

► Ver solución


72. Se fijan los puntos P y R diametralmente opuestos sobre una circunferencia de radio 10 cm de longitud. Sobre cada una de las semicircunferencias, se sitúan dos puntos Q y S respectivamente de manera tal que las cuerdas QR y RS siempre tienen la misma longitud. En la figura se ilustran dos posibles posiciones para los puntos Q y S, denotados como Q, Q y S, S". Con respecto al área máxima que puede tener el cuadrilátero PQRS se puede afirmar que es:
A) 150 cm ²       B) 200       C) 250       D) 300

► Ver solución


73. El sólido de la figura está formado por 3 cubos idénticos, cada uno con aristas de 1 m de longitud. Entre todos los posibles caminos sobre las caras del sólido que conectan los vértices P y Q, el de menor longitud mide:
A) 2+√2  m      B) 4 m      C) √10  m     D) √13  m

► Ver solución


74. La figura está formada por cuadrados de lado 1 unidad. Se desea realizar un corte sobre los lados de los cuadrados, de manera tal que la figura original quede dividida en dos figuras de igual área. De todos los cortes posibles, el de menor longitud en unidades es:
A) 2      B) 3      C) 4      D) 5

► Ver solución


75. En un cuadrado se traza una cuadrícula y se pintan todos los cuadrados de las diagonales de amarillo y todos los cuadrados restantes se pintan de verde. Si el número de cuadrados pintados de amarillo es 41, entonces el número de cuadrados pintados de verde es:
A) 210        B) 400      C) 360        D) 410

Preguntas 76 a 77
Sobre una cuadrícula formada por cuadrados de 1 cm de lado, se construye un Tangram, a partir de un cuadrado de 10 cm de lado, como se ilustra en la figura:

76. El área, en centímetros cuadrados, del paralelogramo (marcado con el número 1) es:
A) 6,25      B) 12,5       C) 14,2      D) 8,3
► Ver solución


77. Si A1 representa la suma de las áreas de los triángulos del Tangram marcados con los números 2, 3 y 5; A2 representa la suma de las áreas del paralelogramo y el cuadrado (marcados con los números 1 y 4 respectivamente) y A3 representa el área del triángulo marcado con el número 6, entonces respecto a estas áreas, la afirmación verdadera es:
A) A1 > A2 >A3         B) A1 > A3 > A2
C. A3 > A1 >A2         D) A1 = A3 = A3
► Ver solución


78.  La figura que continúa en la secuencia

--
Preguntas resueltas del Examen de Admisión a la Universidad del Cauca 2013-II. UNICAUCA.